The so-called Platonic Solids are regular polyhedra. “Polyhedra” is a Greek word meaning “many faces.”

There are five of these, and they are characterized by the fact that each face is a regular polygon, that is, a straight-sided figure with equal sides and equal angles.

It is natural to wonder why there should be exactly five Platonic solids, and whether there might conceivably be one that simply hasn't been discovered yet. However, it is not difficult to show that there must be five – and that there cannot be more than five.

First, consider that at each vertex (point) at least three faces must come together, for if only two came together they would collapse against one another and we would not get a solid. Second, observe that the sum of the interior angles of the faces meeting at each vertex must be less than 360°, for otherwise they would not all fit together.

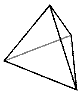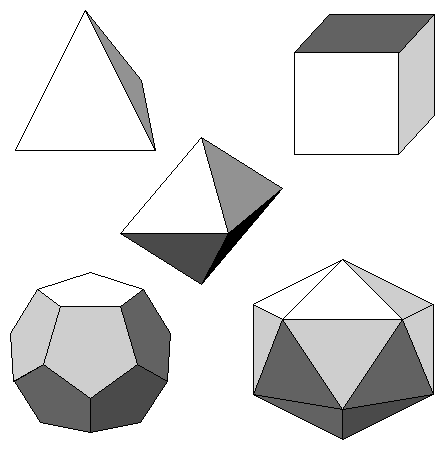
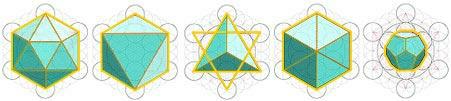
	TETRAHEDRON Four triangular faces, four vertices, and six edges.
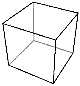	HEXAHEDRON Six square faces, eight vertices, and twelve edges.
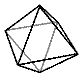	OCTAHEDRON Eight triangular faces, six vertices, and twelve edges.
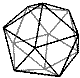
	DODECAHEDRON Twelve pentagonal faces, twenty vertices, and thirty edges.
	ICOSAHEDRON Twenty triangular faces, twelve vertices, and thirty edges.

Now, each interior angle of an equilateral triangle is 60°, hence we could fit together three, four, or five of them at a vertex, and these correspond to to the tetrahedron, the octahedron, and the icosahedron. Each interior angle of a square is 90°, so we can fit only three of them together at each vertex, giving us a cube. (We could fit four squares together, but then they would lie flat, giving us a tesselation instead of a solid.) The interior angles of the regular pentagon are 108°, so again we can fit only three together at a vertex, giving us the dodecahedron.

And that makes five regular polyhedra. What about the regular hexagon, that is, the six-sided figure? Well, its interior angles are 120°, so if we fit three of them together at a vertex the angles sum to precisely 360°, and therefore they lie flat, just like four squares (or six equilateral triangles) would do. For this reason we can use hexagons to make a tesselation of the plane, but we cannot use them to make a Platonic solid. And, obviously, no polygon with more than six sides can be used either, because the interior angles just keep getting larger.

The Greeks, who were inclined to see in mathematics something of the nature of religious truth, found this business of there being exactly five Platonic solids very compelling. The philosopher Plato concluded that they must be the fundamental building blocks – the atoms – of nature, and assigned to them what he believed to be the essential elements of the universe. He followed the earlier philosopher Empedocles in assigning fire to the tetrahedron, earth to the cube, air to the octahedron, and water to the icosahedron. To the dodecahedron Plato assigned the element cosmos, reasoning that, since it was so different from the others in virtue of its pentagonal faces, it must be what the stars and planets are made of.

Although this might seem naive to us, we should be careful not to smile at it too much: these were powerful ideas, and led to real knowledge.

As late as the 16th century, for instance, Johannes Kepler was applying a similar intuition to attempt to explain the motion of the planets. Early in his life he concluded that the distances of the orbits, which he assumed were circular, were related to the Platonic solids in their proportions. This model is represented in this woodcut from his treatise Mysterium Cosmographicum. Only later in his life, after his friend the great astronomer Tycho Brahe bequeathed to him an enormous collection of astronomical observations, did Kepler finally reason to the conclusion that this model of planetary motion was mistaken, and that in fact planets moved around the sun in ellipses, not circles. It was this discovery that led Isaac Newton, less than a century later, to formulate his law of gravity – which governs planetary motion – and which ultimately gave us our modern conception of the universe.

The beauty and interest of the Platonic solids continue to inspire all sorts of people, and not just mathematicians.

 This article is written exclusively by And-El of CrystalWind.ca © 2009-2024 crystalwind.ca. All rights reserved. Do Not Copy.